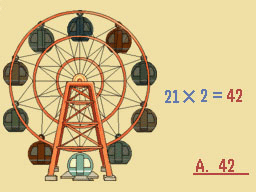[CV087] Ferris Wheel Riddle

←

086 - Squares and Circles

087 - Ferris Wheel Riddle

088 - In a Hole

→

Ferris Wheel Riddle
Game	Professor Layton and the Curious Village
Number	087
Type	Write Answer
Location	Ferris Wheel
Solved by	Luke
Picarats	50
Mandatory	No
Reward	Painting Scrap
In other languages
日本語	観覧車のナゾ kanran sha no nazo
Deutsch	Das Riesenrad
Español	La noria
Français	La grande roue
Italiano	La ruota panoramica
한국의	관람차 수수께끼

Ferris Wheel Riddle is a puzzle in Professor Layton and the Curious Village.

Puzzle

There are 10 two-seater cars attached to the fair's Ferris wheel. The Ferris wheel turns so that one car rotates through the exit platform every minute.

The wheel began operation at 10 in the morning and shut down 30 minutes later. What's the maximum number of people that could have taken a ride on the wheel in that time period?

Hints

• →
• Hint 1
• Hint 2
• Hint 3

Click a Tab to reveal the Hint.

You may think all you have to do is add a few things up, but there's a trick to this problem that's easy to overlook.

Think about the way Ferris wheels have to work. If two people catch the first ride of the day, how much time will pass before they get off the ride?

If the wheel has to stop promptly at 10:30, then the operator won't allow anyone on who can't get off the Ferris wheel by 10:30.

So what does that mean? It means that when two passengers step out of their gondola at 10:30, all other gondolas on the Ferris wheel should be empty as well.

The first pair of people to board the Ferris wheel at 10:00 will get off the ride 10 minutes later. Since the ride itself takes 10 minutes, no one will get off until 10:10. Then, from 10:10 until shutdown at 10:30, people will get off the ride at a rate of two per minute. Calculate the number of people coming off the ride and you'll have your answer, but be careful, because it's easy to make a mistake.

Solution

Incorrect

Too bad!

A car comes once a minute for 30 minutes. Two people can ride in each car.

It certainly sounds simple, but it's awfully easy to overlook some important facts surrounding this problem.

Correct

That's right!

For the first nine minutes the Ferris wheel is moving, the cars arriving at the unloading zone are unoccupied. For the last nine minutes of operation, needless to say, no one will be allowed to board the cars.

From the time the Ferris wheel fills up at 10 minutes past the hour until the last passenger steps off at 10:30, a total of 21 sets of passengers will have taken a ride on the Ferris wheel.